论第二类换元积分法—凑原式与凑递推

   第二类换元积分法，是修高数微积分的小伙伴们都会学到的内容，它也是不定积分中的一个基本的方法之一，大家还记得吗？先让我们来再复习一遍。

   第一类换元，是将f(x)换元成t，常见的有e＾x、lnx、arctanx等。而第二类换元，则是将x换元成f(t)，最常见的就是三角换元，通常，我们看到根号下如果有关于x的平方时会想到。因为三角函数中常有以下两个恒等式：

   所以有：

   不过，知识即使是教下来了，依然有很多同学在换元之后面对恐怖的三角函数军团而束手无策，迫不得已只能用常规方法即尝试凑微分。

   因此，今天带大家带来的就是自己在做题中总结的一些换元和三角处理方法，希望能有帮助。仅是抛砖引玉，如有错误或者不合理的地方勿喷，也请指出。

   如果有更好的方法，欢迎在评论区提出。

   那么就让我们开始叭

   先看这道题，大家应该都很熟悉。每本教材书上基本都有这样的题目作为例题。不过我看到的做法，很多都是常规的不换元做法，不知道你们习惯什么方法呢？

   x的方加常数，那么就令x=atant，整理得：

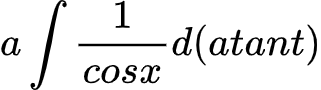
   这里直接分部积分，因为如果d后面的函数展开来，一会还要再进去，即：

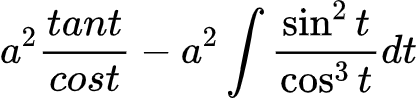
   乍一看感觉更复杂了，不过如果注意到sin＾2（x）+cos＾2（x）=1，获得以下式子。如果之前那个式子有试过把tant拿出来的，可能会发现，其中有一项就是我们要求的。

   这就是我们今天要说的核心了。

   因为三角函数的几个特性，一是不同函数存在很多关系，二是不同三角函数的导数相互等于对方，三是三角函数降次、升次有很多方法，所以会产生在算着算着出现“原式”的情况。

   接下来就是1/cosx的积分。这个书后的积分表都有，方法也多种多样，我用最容易懂的方法再过一遍。

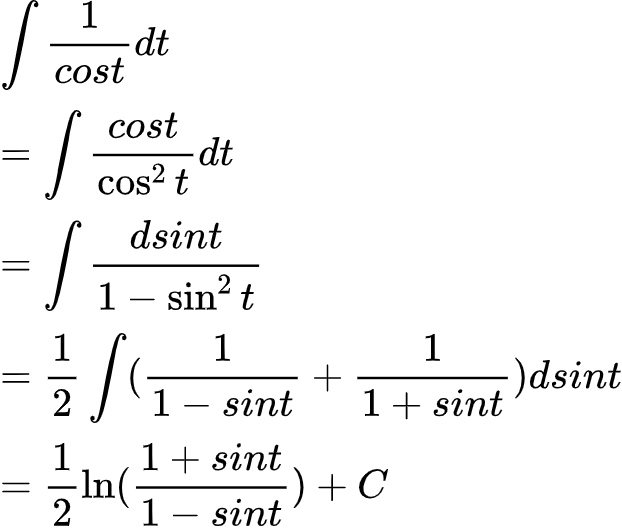
   之后求出原式的结果，合并：

   最后一步代入，一定要细心不要功亏一篑，最好的方法是把三种三角函数关于x的式子列在草稿纸上对照，即：

   得出结果：

   上述题目，可能会有人觉得还是常规方法比较简洁，但是倘若在考试的状态，一开始只想到了三角的话，还是要继续算下去。因此，这个方法是必不可少的，而且，题目有时候也会出纯三角的题。

   那么，由一道题目，引出的，就是核心内容：

   不定积分中三角式的凑出原式与降次递推

   说到降次，教材里有这么一道题，sin＾m（x）的不定积分。方法就是用到了我说的，即：

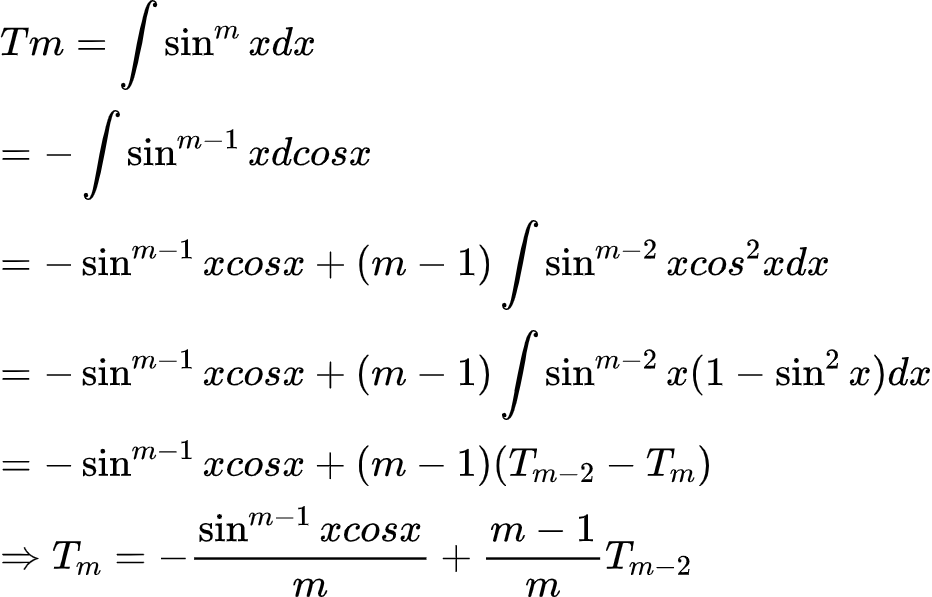
   其实我的题目用到的方法有异曲同工之妙。

   不妨来对比一下。

   第一步：将可以凑出微分的式子提出来

   第二步：分部积分

   第三步：将分部积分的结果中的积分部分用各种公式尽可能地往“原式”结构靠拢，并得到另一个降次的积分式。

   那么，接下来，我们就把它变成倒数，再来求一次递推吧。

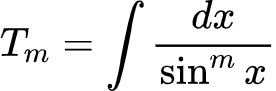
   这次怎么降次呢？我们要降的是分母，既然1/cos＾2（x）是tanx的导数，那么，1/sin＾2（x）就是-1/tanx的导数。

   这里插一句题外话，我不是特别喜欢用另外的三个三角函数（cot、sec、csc)，一是容易出错，二是不好观察结构。

   同样，分部积分得出以下式子，看吧，又出现cos＾2（x）了，变成1-sin＾2（x），得到类似的结果。

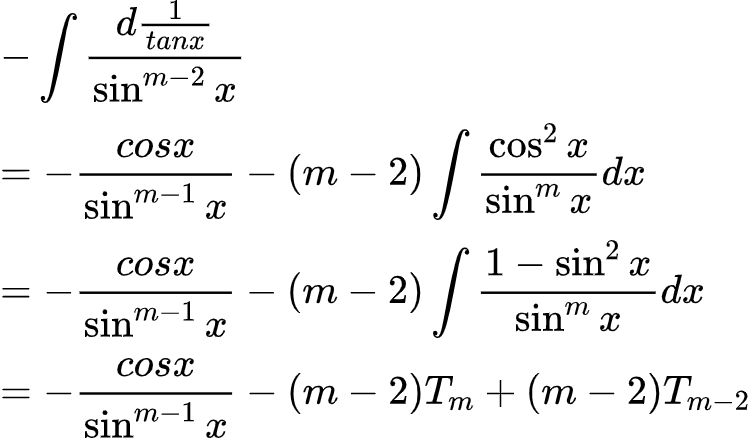
   所以就可以得出

   将sinx替换成cosx（将x替换π/2-x），同理，可以得出

   就是热身题的式子啦（m=3）。

   还没结束，接下来，我们来试试更一般的结构。

   这里，我们要的效果是m和n一起降次，那么，如果单独凑sinx或者cosx是不行的了。那么，我们要提取出来的式子，必须是sinx的某次方/cos的某次方。那么，导数中既有sinx也有cosx最简洁的函数是什么呢？

    我选择的是1/cosx，导数为sin＾x/cos＾2（x）。

   同样，凑微分，分部得

   有些复杂，不过处理方法还是不变，不过这里就不需要再代换啦，因为已经凑出来递推了。即

从而

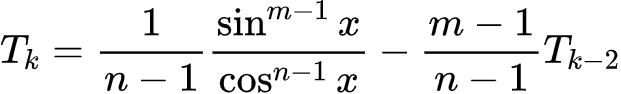
   那么，说了那么多，每个的式子都很复杂而且也没有规律

   不过它们不必要记下来，但是需要掌握其中的方法。

   下次（如果还有下次）会给大家带来一些自己觉得和这个比较一致题目，全部来源于网上，可能部分题目有一定的难度。不要担心，考试绝对不会考这么难。