目录
注:本文后面较为抽象,观看可能会出现以下两种状况:
1头脑发昏、轻微的烧脑
2对生命、对人生的迷茫
请量力而行,谨慎选择性地观看。
但是,短短的几十年,即使我们无法穷尽一切的未知与真理,我们也能通过自己,让人生在茫茫宇宙中留下绚丽的浓墨重彩。
既然是大数,我们先来个引子。
假如给你们3个3,用特定的运算组成一个你觉得最大的数字,那会是什么呢?
刚上一二年级的小学生,会说是3+3+3=9,后来学习了乘法,就说是3x3x3=27,再后来,学习了乘方,就会说是(3^3)^3=3^9=19683。似乎到这里,已经是能用简洁形式表现的最大数了。
但是,不知道你们有没有看过这样一种数,数学书上有个说2^2^5+1为合数,这里不讨论它是否为合数,只是,你们有没有觉得它有些大得离谱?这是一个更进一步的运算,超乘方,即:
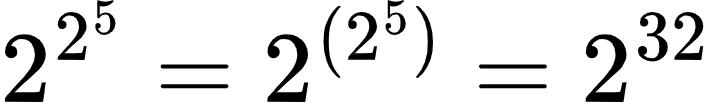
它和(2^2)^5=2^20不同,超乘方是从上往下计算乘方,因此如果数字足够大,或者是叠的层数足够多,它会比所谓“幂的乘方”要大的多。那么,倘若把3个3用超乘方来表示,那么就会出现:
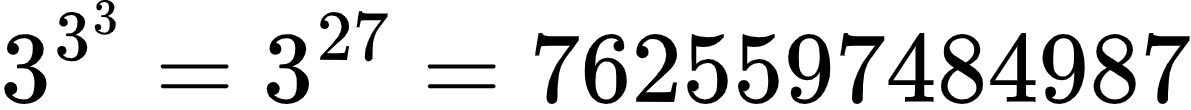
这个可比3^9,也就是19683大好几个数量级。如果再叠一层,则会有差不多7.6 x 10^12个3连乘,常规的手机计算器都算不出来了。因此,超乘方的每一次套娃,数量级都呈现惊人的增长。
不过,别以为这样就完事了,这些数字,比起接下来要讲的,那真的是用宇宙中的沙子来比喻,都显得很大了(不是夸张哦)。
在上个世纪,随着计算机程序的出现和发展,人们逐渐意识到,随着运算的复杂度的提升,原先的那些运算无法支撑起庞大的体系,于是,我们就出现了所谓的高德纳箭头,用多个指向上的箭头表示。是由计算机方面的专家高德纳提出的。
我们来看看它的定义:
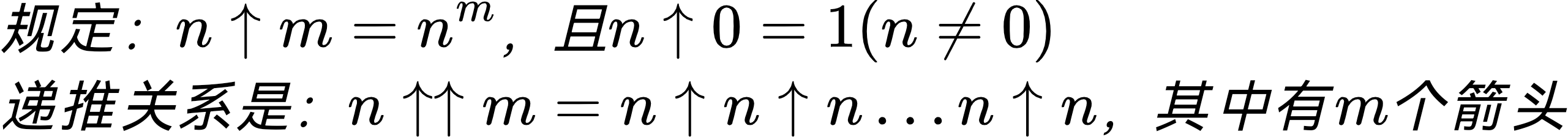
要注意的是,右边的式子和超乘方一样,要从后往前算。
那么,如果用3来表示的话,则
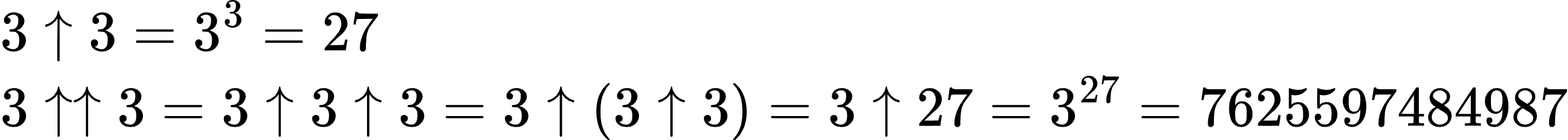
有些人可能感觉还好,还能表示,但是,如果我们再加一个箭头的话,会得到:

是不是有些不对劲了?是的,这个数字大到,连用超乘方都得用省略号。如果,我们非要写完整,假设每叠一层要写2 cm,则总长度为1.5×10^11 m,按高度来算,就要写到太阳上(地日距离为1.49 x 10^11 m)
接下来,我们来算4个箭头的,由于某些符号在软件上用不了,所以我只能改手写了。
最后结果就是这么一个东西。
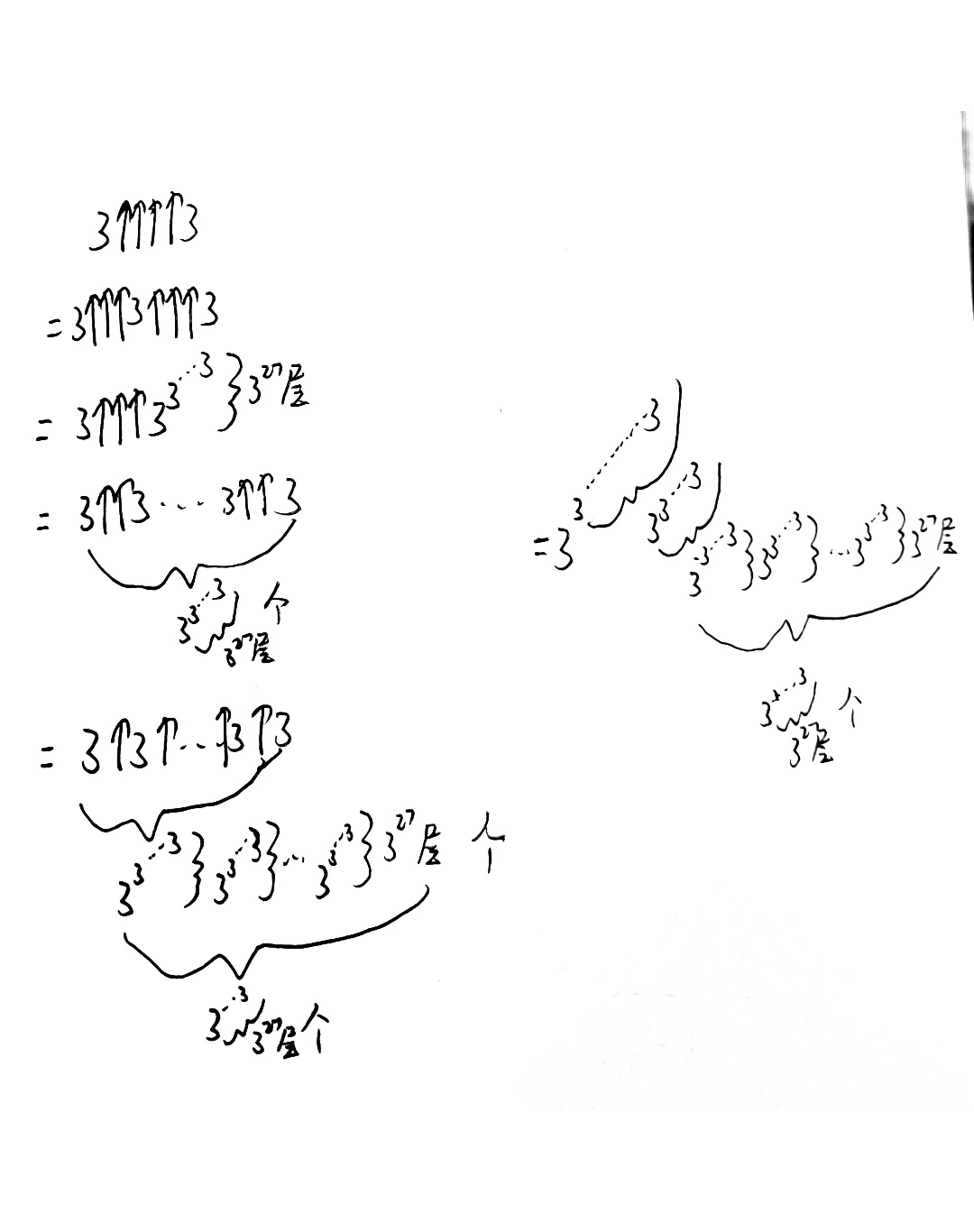
没错,大到离谱了,都不知道套娃的套娃的套娃叠了多少层套娃。大到什么程度呢?这个数字的位数的个数都无法用正常数字表示出来,甚至连位数的位数的位数的位数…都无法表示出来。
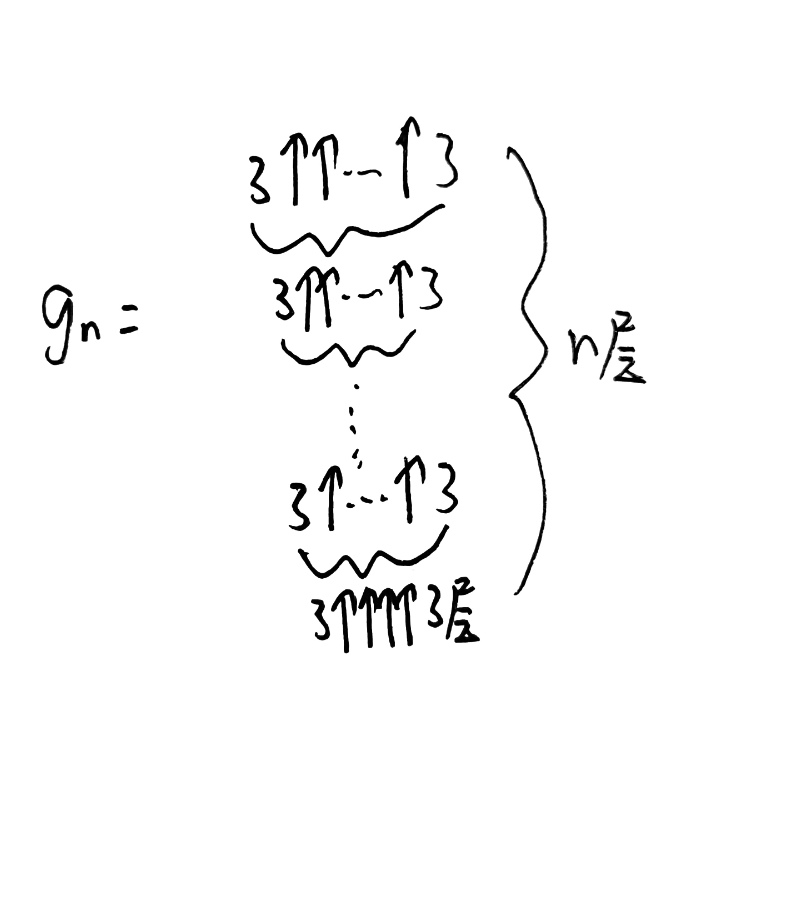
那么,知识点扩充完了,让我们来进行今天的主话题:gn
gn呢,简单来说就是高德纳箭头套娃。比如刚才的四个箭头的,就是g1。
我们规定:
接下来就是第一个有意义的大数,葛立恒数。
它的定义是,多维四方完全图(多维四方完全体:多维空间里的多维立方体中每个顶点都与其他的每个顶点直线相连)的每个连线用两种不同颜色标记,能保证在所有标记法中,取任意四个顶点都不会出现相同颜色的完全图的最大整数。
此时gn中的n为64,即g(64),也被称为graham。这个数字早已大到人们难以想象。因为即使是最下层的那个数字的表示,都如此的困难。
这个数字大到什么程度。回到我们刚才所说的沙子填宇宙,不过沙子还是太大,现在我们最小的度量单位,普朗克长度,也就是1.6 x 10^(-34)m,目前可观宇宙的直径为920亿光年,也就是9 x 10^26 m。如果把宇宙当作正方体,那么它能装下10^182个数量级的普朗克常数为边长的正方体。这个数字简直不要太小,它甚至远远不及最下层的那个数字套娃的层数。即使算上不同时空的不同平行宇宙(大约10500),能给这个极小的数字增加的数量级也是微不足道的。
有人估计,如果将葛立恒数的所有数字强行让人脑记下来,那么人脑会变成黑洞。
这个数字大到的程度,我们无法写出它的位数,它的位数的位数的位数…都无法写出来,最可怕的是,要套多少个“的位数”,都是不知道的。
因此,围绕着葛立恒数,我们可以自己组建更大的数字,比如g(65),甚至是g(graham),给它套葛立恒数个套娃,更有甚者,不断套葛立恒数的层数为葛立恒数。
那么,让我们向更大的数前进,fΦ(1),它就是上面的那个套娃,即

再规定:
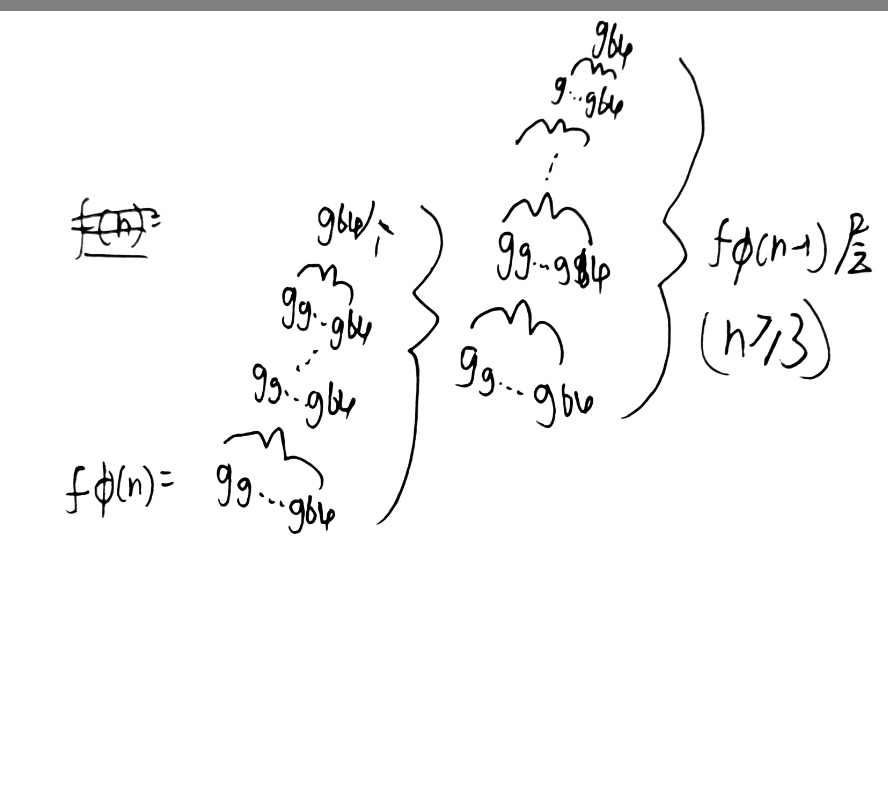
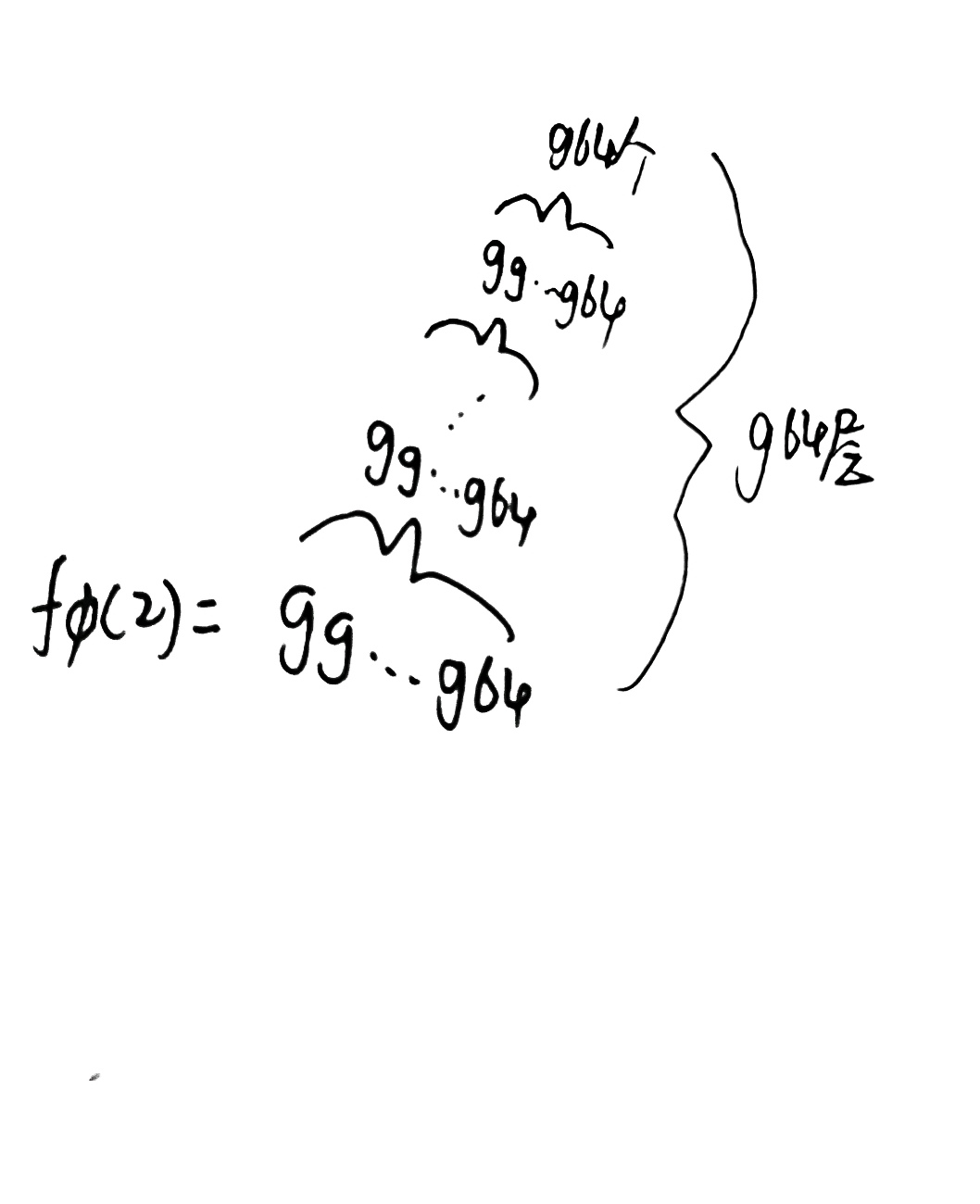 是不是很像刚才的那个高德纳箭头的形式?只不过这次套的是葛立恒数而不是微不足道的乘方。每套一个“g”,可以想象到,那数量级的增长…
是不是很像刚才的那个高德纳箭头的形式?只不过这次套的是葛立恒数而不是微不足道的乘方。每套一个“g”,可以想象到,那数量级的增长…
不过,我们这次不从n下手,继续从fΦ(1)中的“Φ”下手,规定:
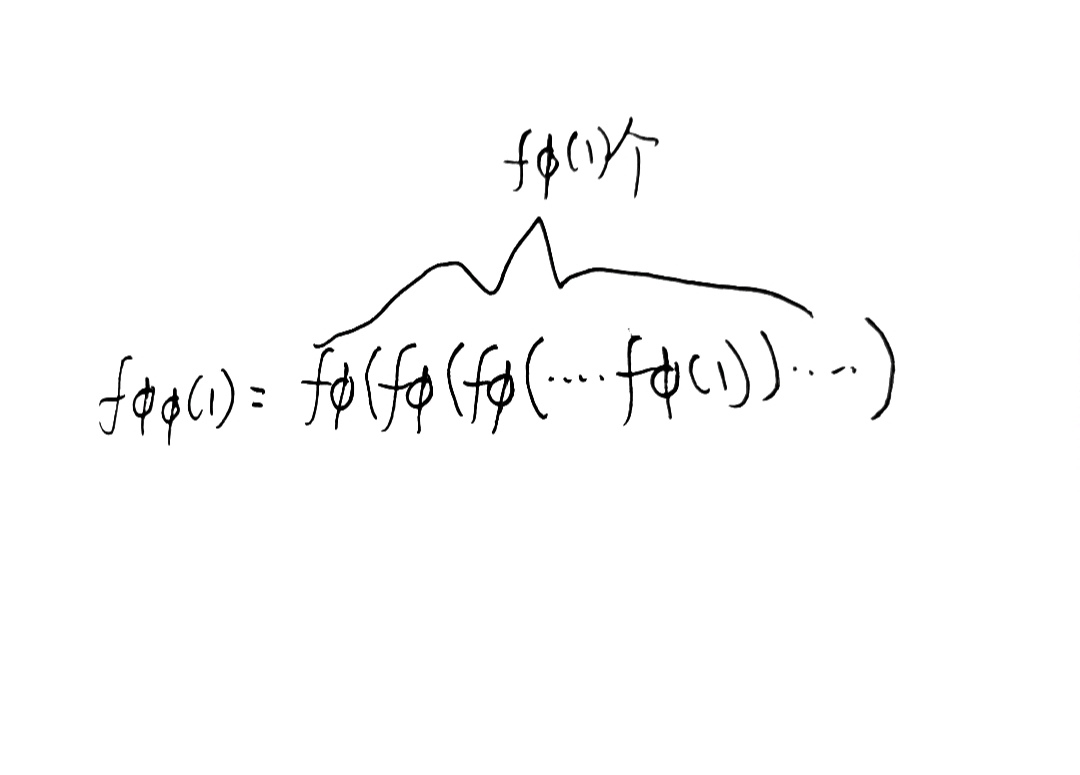
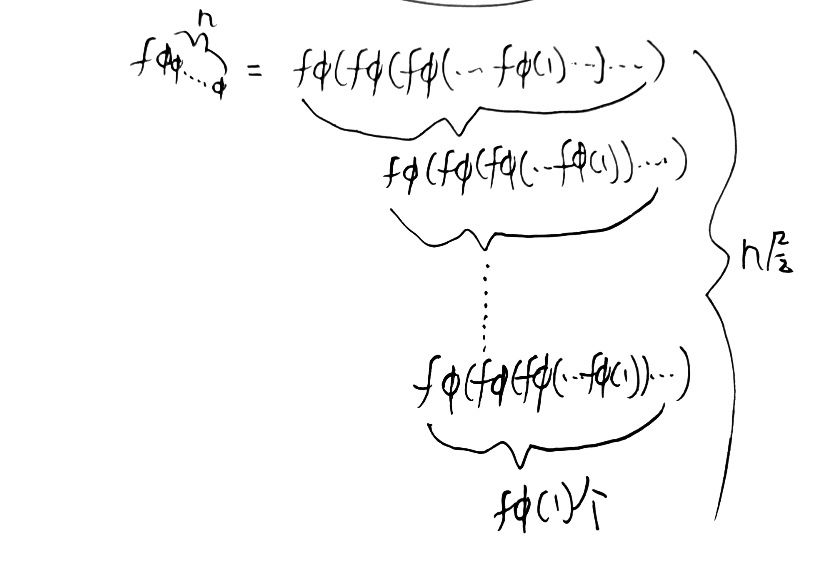
很像葛立恒数类数字的套娃,但是这次套的也不是小小的高德纳箭头,而是每加一个都会大到惊人的数不清的葛立恒数。
如果止步于此,那么还是有些肤浅。科学家们继续研究,得出了更大的有意义的数字。那就是著名的tree(3)。
这个数字等于上图的n等于187196时的大小。
那么复杂的数字,也是有它的定义的。
我们先从tree(n)说起,既然是tree那么它一定和树有关。此树,就是用那种连线分支来表示,tree(n)代表的是,用n种不同的颜色画树时,树的总数。但是它还有规则,规则如下:
1第一棵树只能分一次,第二棵不超过两个终结点,第n颗不超过n个。
2后面的一颗,任意取其中的一部分,不能出现与前面重复的树(颜色、分支完全相同)。
从tree(1)画起,可知tree(1)=1,tree(2)=3但是从tree(3)开始,我们就会发现,再怎么努力貌似都画不完了。也从上面可知,tree(3)大到可怕,所以不要做这样的尝试了。
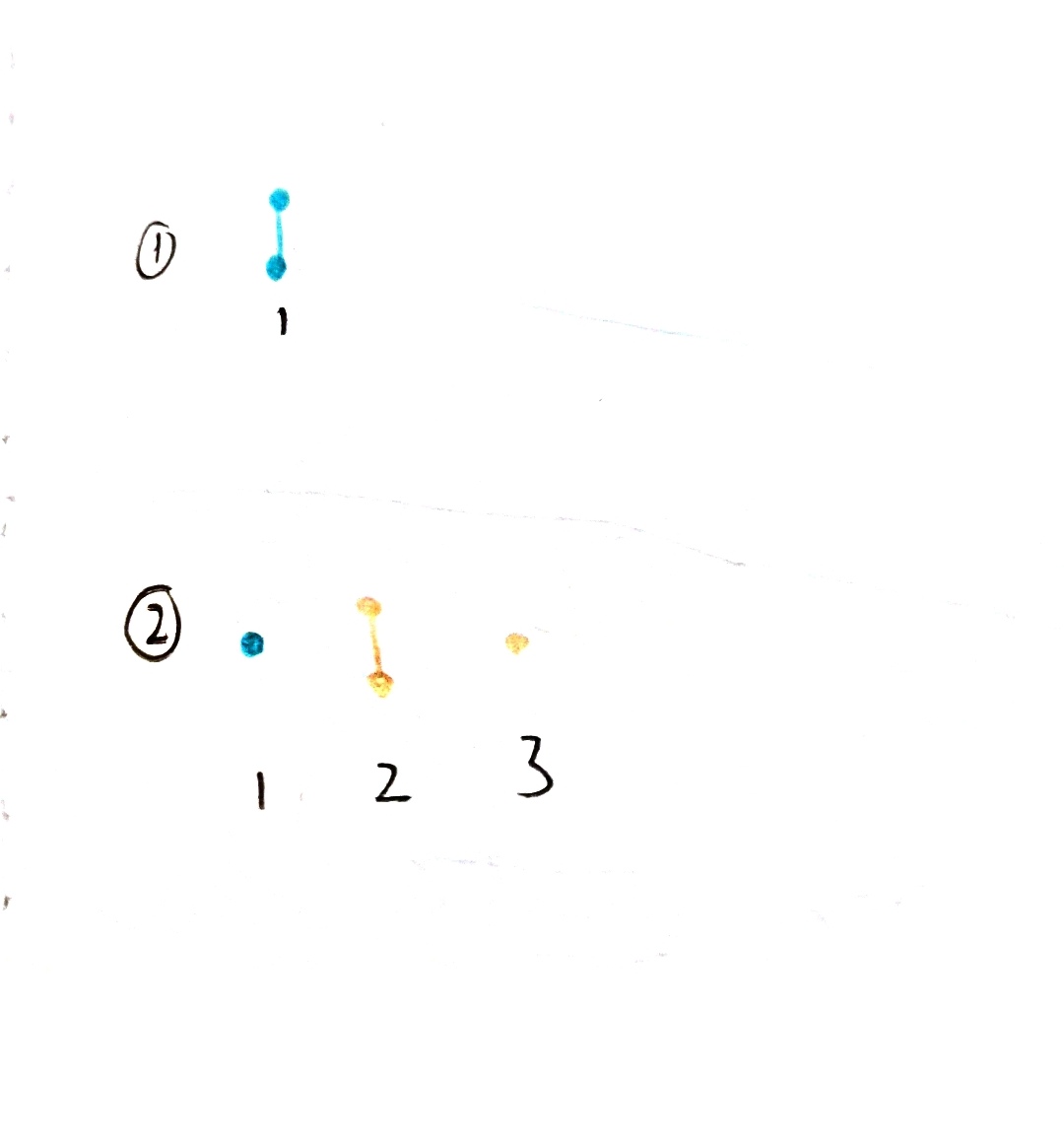
可见,和tree(3)比起来,葛立恒数乃至fΦ(1)都是极其小的一个数字。
之后,便有了g(tree(3)),tree(4),tree(tree(3)),叠tree(3)次的g(graham)、fΦ(1)等等等等,特别注意的是,g(tree(3))小于tree(4)。
到此,以上的数字还能为人们所理解,那么接下来的,就是完全完全抽象的了。
(以下取自于本人对各种资料的翻译和解读,可能会有不对的地方。)
首先是所知的最大的有意义的数字,sscg类,这里的话相关的信息很少,大概看了一下,就是关于n个数字数字位数嵌入时,最多的种数。典型的就是sscg(3)。
接着,才到了正戏。
已知的最大的有意义的数字,是rayo number,其介绍也没有确切的资料,里面大多都是…计算机语言,懂的小伙伴可以去翻译一下,链接:https://googology.fandom.com/wiki/Rayo%27s_number
最后,正式地到了无限的表示,阿列夫。
其中,阿列夫0( א 0)表示的就是,所有的实数的集合。包括了以上涉及到的所有神仙们。
之后,还有阿列夫1,2,3…
阿列夫1:二维空间里所有点的集合
阿列夫2:三维空间里所有曲线弯曲可能的合
阿列夫n:n维空间里所有可能的点集
倘若,阿列夫到极限,所表示的就是无穷维空间里的点集。
之后,就是各种所谓的“不可描述”的无穷大,例如欧米茄等。
经历过这些之后,事物达到了最后的绝对无穷,∞,一切,宇宙的万物,宇宙本身,都将归于虚无。



![[下载/搬运/纪录片/熟肉]Homotherapy(以爱之名:同志矫正治疗)[1080P][已完结][内嵌][2.73G][2019]](https://yuri.website/wp-content/uploads/thumb/2022/02/fill_w372_h231_g0_mark_p2632286342.jpg)


![[下载/搬运/文学研究/汉译][桑梓蘭] The Emerging Lesbian: Female Same-Sex Desire in Modern China(浮現中的女同性戀——現代中國的女同性愛欲) [王晴鋒译] [臺大出版中心][已完结][2014]](https://yuri.website/wp-content/uploads/thumb/2022/01/fill_w372_h231_g0_mark_1939a99778c51976e_1_post.jpg)




![[安利/安价/熟肉]组曲&哈士奇考古笔记[未完结][2008]](https://yuri.website/wp-content/uploads/thumb/2024/03/fill_w372_h231_g0_mark_455d38d4bfa7166_1_post.jpg)
![[安利/动画/熟肉]航向未来的祝愿【2023年灯子祭/视频合集】[2023]](https://yuri.website/wp-content/uploads/thumb/2023/02/fill_w372_h231_g0_mark_358de316f6bb751c_1_post.png)
![[安利/游戏/熟肉]Yu-Gi-Oh!Master Duel(游戏王:大师决斗单机版)[8GB][2022]](https://yuri.website/wp-content/uploads/thumb/2023/01/fill_w372_h231_g0_mark_82218a7b6f330a3_1_post.jpg)
![[安利/音声/熟肉]ユビノタクト TS百合系列 资源汇总/剧情时间线整理](https://yuri.website/wp-content/uploads/thumb/2022/10/fill_w372_h231_g0_mark_24783a45c0b3d2fc6_1_post.jpg)
![[在线/同人/小说]【既往章节整理】+寒河江满[御景柚姬][歌手小松未步的同人]](https://yuri.website/wp-content/uploads/thumb/2024/04/fill_w372_h231_g0_mark_14350656aee7f63b06_1_avatar.jpg)
![[在线/同人/小说]Love is a bird (1)+寒河江满[歌手小松未步的同人][御景柚姬][长篇]](https://yuri.website/wp-content/uploads/thumb/2024/04/fill_w372_h231_g0_mark_14350146c1a1e3fbc6_1_post.jpg)
![[在线/同人/小说]我放不下你(1)+寒河江满[御景柚姬][歌手小松未步的同人]](https://yuri.website/wp-content/uploads/thumb/2024/04/fill_w372_h231_g0_mark_143505e8266204ea6a_1_cover.jpg)
![[在线/同人/小说]回忆+寒河江满[歌手小松未步的同人][御景柚姬][长篇]](https://yuri.website/wp-content/uploads/thumb/2024/04/fill_w372_h231_g0_mark_143502e06e663d7275_1_post.jpg)
![[在线/同人/绘画] 杏豆 [MaidCode1023][世界计划同人]](https://yuri.website/wp-content/uploads/thumb/2024/03/fill_w372_h231_g0_mark_4538c60304fc6588_1_post.png)
![[在线/同人/绘画] 仙宫11 [MaidCode1023][一周一次买下同班同学的那些事同人]](https://yuri.website/wp-content/uploads/thumb/2024/03/fill_w372_h231_g0_mark_45336e09240f25c6_1_post.png)
![[在线/同人/绘画] 碧碧x艾米 [MaidCode1023][我爱艾米同人]](https://yuri.website/wp-content/uploads/thumb/2024/02/fill_w372_h231_g0_mark_453c6f6555d8aa27_1_post.png)
![[在线/同人/绘画]约稿同人:真机伶×清水樱 情人节贺图[约稿][赛马娘同人]](https://yuri.website/wp-content/uploads/thumb/2024/02/fill_w372_h231_g0_mark_2532e68ccbcc9d59e_1_post.png)
![[在线/首发/漫画/熟肉][筋肉☆太郎]飛野さんのバカ(飞野同学是笨蛋)[提灯喵汉化组][GANMA][连载至第111话][2018]](https://yuri.website/wp-content/uploads/thumb/2024/04/fill_w372_h231_g0_mark_4b2d7631-692e-4af2-abc3-be8eee566eaa.jpg)
![[在线/首发/漫画/熟肉][棘尾どろしー]見えてますよ!愛沢さん(我看得见哦!爱泽同学)[提灯喵汉化组][コミックヴァルキリー][连载至12 堪称完美][2022]](https://yuri.website/wp-content/uploads/thumb/2024/04/动画化拉票fill_w372_h231_g0_mark_1.jpg)
![[在线/首发/漫画/熟肉][なもり]ゆるゆり(摇曳百合)[提灯喵汉化组][コミック百合姫][连载至第197话 朦胧女子][2008]](https://yuri.website/wp-content/uploads/thumb/2024/03/fill_w372_h231_g0_mark_resize_image-3.jpg)
![[在线/首发/漫画/熟肉][シクシク]この世で一番素敵な終わり方(这是世上最美好的落幕方式)[提灯喵汉化组][コミック百合姫][连载至10.5 第二卷添笔][2022]](https://yuri.website/wp-content/uploads/thumb/2024/03/fill_w372_h231_g0_mark_DL-Raw.Se_001.jpg)
![[在线/首发/小说/熟肉]まな板のうえの恋(砧板上的爱/Love upon the Chopping Board)[发布者自译][6/15][1993]](https://yuri.website/wp-content/uploads/thumb/2024/02/fill_w372_h231_g0_mark_13537ac46652cba3ed_1_post.jpg)
![[在线+下载/搬运/小说/熟肉][あらおし悠、铃音れな] 百合ラブスレイブ わたしだけの委員長(百合爱的奴隶 只属于我的班长)[江东][キルタイムコミュニケーション][已完结][epub][2018]](https://yuri.website/wp-content/uploads/thumb/2023/12/fill_w372_h231_g0_mark_1306525db3164564c0_1_post.jpg)
![[在线+下载/搬运/动画/生肉+熟肉]海のまにまに(任由海波荡漾)[Aki惊蛰][4K][1080P][已完结][YouTube][Bilibili][MV][YOASOBI][2023]](https://yuri.website/wp-content/uploads/2023/03/999.gif)
![[在线/转载/纸动画][推特]爱的日子[21MB][2022]](https://yuri.website/wp-content/uploads/thumb/2022/05/fill_w372_h231_g0_mark_MGT@0U4YYIRU6TA@QSN.png)
![[在线+下载/首发/音声/熟肉]【魔法少女にあこがれて】【ASMR】マジアベーゼにいたずらされて【耳ふー・咀嚼音・耳かき】(【憧憬成为魔法少女】【ASMR】魔法枫糖的恶作剧时间【吹耳 · 咀嚼音 · 掏耳】)[YouTube][百合音声同好会][2024]](https://yuri.website/wp-content/uploads/thumb/2024/01/【魔法少女にあこがれて】【fill_w372_h231_g0_mark_ASMR】マジアベーゼにいたずらされて【耳ふー・咀嚼音・耳かき】-KADOKAWAanime-1.jpg)
![[在线/首发/音声/熟肉][RJ307502]どうしていつもこうなるのっ!?(为什么总是会变成这样啊!)[百合音声同好会][2020]](https://yuri.website/wp-content/uploads/thumb/2022/09/fill_w372_h231_g0_mark_37NG6581JV1_7UQ9P.png)
![[下载/首发/音声/熟肉][YouTube]不会死去的她与忧伤的雨天[百合音声同好会][2021]](https://yuri.website/wp-content/uploads/thumb/2022/08/fill_w372_h231_g0_mark_PMH8X4FYWW_IW2K8NM92.png)
![[下载/首发/音声/熟肉][RJ246088]ランドリー(White Laundry Magnolia)[百合音声同好会][2019]](https://yuri.website/wp-content/uploads/thumb/2022/08/「ランドリー」イメージイラストfill_w372_h231_g0_mark_.jpg)









看到一半直接划到评论区,原来大家跟我一样,那放心了